Featured Book
Numbers and the Making of Us
Counting and the Course of Human Cultures
Caleb Everett
Hardcover edition 2017
There are predictable numbers in nature, but we humans have an innate, “exact” number sense for numbers only up to three. Beyond three, we can tell when groups of objects are more than or less than one another, but the exact numerical correspondences between quantities are concepts we have to learn. Anthropologist Caleb Everett suggests that “numbers” or “the words and other symbols for specific quantities” are “a key set of linguistically based innovations that has distinguished our species in ways that have been underappreciated. … They have reshaped the human experience.”
Even in Paleolithic times, we realized that keeping track of aspects of the natural world might improve our chances of survival. We’ve been recording quantities, using prehistoric numerals, for tens of thousands of years. 44,000-43,000 years ago someone in the mountain ranges between South Africa and Swaziland carved twenty-nine lines into the side of a baboon fibula, perhaps to track the days in a lunar cycle; in France a 28,000-year-old bone known as the Abri Blanchard plaque bares engravings that may also represent phases and movement of the moon; and a 10,000-year-old reindeer antler found near present-day Miami bears tally marks that quite likely refer to quantities, such as days or moon cycles.

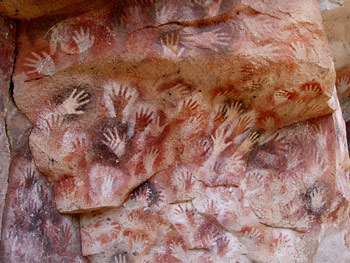
Because we are bipedal animals, our hands are free to serve other purposes including acting as our personal counting tools. The invention of numbers is attainable by the human mind first through our fingers. Linguistic data, both historical and current, suggest that numbers in disparate cultures have arisen independently through the realization that hands can be used to name quantities like 5 and 10. Everett sees the preponderance of stenciled hands in cave paintings as possible evidence of finger counting.

About 8,000 years ago, as specialization due to agriculture occurred in the Fertile Crescent, it became necessary to precisely record amounts of produce and livestock so that they could be bought, sold or exchanged. Clay containers filled with clay tokens, each representing say one animal or a specific quantity of grain, were used to formalize contracts between Mesopotamian traders. The container would need to be broken in order to find out whether the contract had been honored. Over time traders’ invented symbols representing the number of tokens inside the container which they wrote on the outside; and eventually the tokens were dispensed with altogether in favor of written numbers. Mathematics and writing developed in parallel, each one stimulating the other. Verbal conversations relating to trade and other matters could now be written down. “By 3,600 years ago, Babylonians were already utilizing algebra and geometry, solving quadratic equations, and had already discovered π (at least approximately). So the representation of quantities seems to have ignited the development of Sumerian writing, which in turn eventually yielded the capacity to more elaborately represent quantities,” says Everett.
Different number systems evolved in different parts of the world, and where that happened, the idea of writing down numbers and what this could lead to spread; at least one hundred systems for writing numbers have been documented worldwide, many of which no longer exist. The use of numbers in speech is ancient and common to nearly all languages. Nevertheless, whether developed in Europe, China, India or Mesoamerica, these “number words” tend to involve our body parts. Hands (and to a lesser extent toes) were initially used for counting and are still relied upon; as a consequence, most number systems are built on bases 5, 10 or 20, the most common being base 10.
Number words for quantities above five are often phrasal. In Karitiâna, a language spoken in Amazonia, the number six is represented by “take one and our other hand.” Most number systems rely on addition or multiplication to construct larger quantities. In Mandarin, 11–19 are additive, that is people say 10 plus 1, 10 plus 2, etc., whereas 20, 30, 40, and so on are multiplicative. In many languages, addition is denoted with words such as “take” or “seize”; in Karitiâna, for example, the word for 11 can be translated as “take our one toe.”
The Sumerians and Babylonians used base-60, which is the reason we divide hours into 60 minutes and minutes into 60 seconds. Base-60 seems an unlikely choice until we consider that it is divisible by 5, 10, and 12. It is easy to see why many number systems are based on 5 and 10, but 12 is less obvious. It is only when we realize that a human hand has four fingers each with three segments that the significance of 12 becomes apparent. In some parts of New Guinea counting terms are based on the entire body, not just the fingers and toes. One counting system has 27 numbers corresponding to various parts of the body.

As we’ve said, humans everywhere can quickly distinguish small quantities of 1 to 3 without any training, but for quantities greater than 3, we can only distinguish differences if they are significant. An eye-witness may not be able to remember whether there were 6 or 7 assailants but will certainly respond correctly if the difference is between 6 and 12. Counting allows us to accurately distinguish larger quantities, so if that same witness happened to count the number of assailants, he or she could accurately respond when questioned. Our limited innate neurobiology helps explain why what linguists refer to as “grammatical number”:
- can be found in the vast majority of languages
- tends to distinguish 1 from other quantities
- refers to larger quantities in an approximate way
Numbers don’t just come into language in the form of words or symbols for numbers. Quantities can also be inferred by the plurals of nouns, or in the forms of verbs. Ninety percent of the world’s languages have a way of distinguishing between one and many. Nouns may change form depending on whether we are talking about a single item or many, as in one “person” or several “people.” In English we are used to the idea of adding an “s” at the end of a word to make a noun a plural. This is common across many languages, “gato” changes to “gatos” in Portuguese. Plurals can also be formed with prefixes (at the start of the word), and even “infixes.” For example, in the Tuwali Ifugao language woman is babai but women is binabai. The plural is formed by adding -in- within the word.

Additionally, verbs and pronouns change to show agreement with the subject of a sentence, for example, we say, “my car is fast,” and “our cars are fast.” Languages have number-like words for specifying approximate quantities, for example we have several words in English such as a couple, a few, several, many, and so on. Languages have words that indicate more than one of a specific type of object, such as a “herd” of animals, a “school” of fish, and a “flock” of birds. Grammatical number is in virtually all languages, requiring people to continually refer to quantities – some may seem quite unusual to us. For example, if a Boumaa Fijan speaker in a village of sixty people is communicating with a few or even over a dozen other people, she will use the “paucal” second person pronoun, dou. In contrast, if she is communicating with everyone, she will use the plural second person, omunuu. A small subset of the world’s languages use what are called trial inflections, used only when exactly three items are referenced.
The limited innate sense that we have for number is borne out by studies of anumeric peoples, like the Pirahã, a small group of hunter-gatherers who live deep in the Amazon rain forest whose society evolved without numbers. Everett emphasizes that this was not because of any mental deficiency – in more recent years, having been exposed to numbers, they have chosen not to change; they see no reason for them. The language they speak has no precise number words, not even “one” or “two.” It also lacks grammatical number terms like “both,” from which you can tell whether the speaker is referring to two of something. While the Pirahã do have some number-like phrases, they are ballpark expressions, like “a few” in English. If you show them a lineup of seven spools of thread and ask them to replicate it, they struggle when creating lineups of five or six or eight. They can tell that a large group of spools is bigger than a much smaller group, but their exact number sense ends after 3. This means that they don’t require quantity differentiation in their housing structures, hunting implements, or in creating or quantifying small artifacts. In fact, they don’t use precise quantity differentiation for any of the tasks in their culture, which, for those of us immersed in a world of numbers is hard to conceive.
Because we are so locked into seeing the world through numbers, we might wonder how for example, Pirahã parents know the age of their children or even how many they have? Everett points out that since every child is known as an individual, and is remembered including the event of his birth, there’s no need to know the number of children anyone has or knows.
Deaf people who have not learned sign language are often anumeric. They use hand gestures to talk to those around them, but their communication often lacks number words. Such is the case with a group of deaf Nicaraguans who have, for a variety of reasons, never had the opportunity to learn a sign language. Instead, they use innovated hand gestures to speak with those around them. Unlike the Pirahã, they live in a numerate culture, and understand the importance of differences between quantities. They can recognize the approximate values of monetary notes and are capable of differentiating smaller and larger bills. Yet, despite such an awareness, and despite their awareness of the existence of precise quantities beyond three, they don’t have their own means of referring to such quantities in precise ways. Like the Pirahã, they show no sign of any cognitive disability, but they obviously had no opportunity to learn number words and practice using them until they could consistently and exactly differentiate quantities greater than three.
Perhaps the most convincing evidence of our limited innate numeric ability comes from cognitive research on children. Since humans, including infants, stare longer at unexpected or new events, child development psychologist Karen Wynn hypothesized that infants would stare longer at impossible outcomes. She wanted to test whether 5-month-old infants have the ability to add 1+1 and found that when one item was added to another, but the outcome was only one item the infants were perplexed and stared longer. In fact, they stare significantly longer at the impossible outcome. It is now recognized that infants can differentiate three items consistently.
A study by psychologists Fei Xu and Elizabeth Spelke demonstrated that infants can recognize quantitative differences in large sets if the ratio between compared sets is significant. Infants six months old can recognize the difference between 8 objects and 16 objects. However, when they tested the infants’ ability to recognize the disparity between arrays of 8 and 12 dots, instead of 8 and 16 dots, reducing the ratio of quantities to 2:3 (8:12) from 1:2 (8:16), the results shifted dramatically. The infants’ staring patterns reflected no appreciation of the disparity between 8 and 12 dots. This is compelling evidence confirming that infants can recognize differences between large sets of quantities when the ratio is a least 1:2 which suggests that humans have an innate ability for approximating large quantities.
Recognizing the difference between one and two doll-like figures, or between 8 and 16 dots on a screen only implies that infants are drawn to visual disparities. Recent studies have attempted to study cross-modal recognition of quantities by infants. Psychologist Veronique Izard and her colleagues have demonstrated that newborn babies can recognize some differences between quantities on an abstract, cross-modal basis. After Infants heard a sequence of four syllables, they stared longer at a screen that displayed four images than one that displayed either eight or twelve images. The findings of Izard and her colleagues support the claim that humans are born with the ability to approximate large sets of items, and that this ability is tied to more than one of our senses.

A team of psychologists at the University of Chicago studied the numerical gestures of children 3-5 years old. The children were more at home using their fingers to describe small quantities than using number words. Fingers can represent the number of items in a small set, whereas number words are arbitrary and must be memorized. 3-year olds learn number words but have only a very basic understanding of what they mean. By the age of four, children learn the successor principle, which refers to the awareness that each number in a counting sequence is one more than the previous number. Another milestone on the way to arithmetic thought is the cardinal principle. When children acquire this principle, they recognize that the last number in a counting sequence represents the quantity of the entire set.
The use of words to represent numerical concepts greatly enhances our ability to manipulate numeric quantities but getting to this stage is hard work and is acquired over the course of many years. When children learn numbers, Everett emphasizes, it can’t be a process of learning names for concepts they already have. It must be a process of “concepting” those names: words like “four” and “five” and “six” function as place holders for ideas children eventually grasp. With instruction and practice, they start with concepts they know intuitively (such as that 2 is one more than 1) and learn to construct others by analogy (such as that 8 is one more than 7). Much as a fishing rod is a tool we use to acquire fish, number words are tools we use to acquire number concepts.
What about the numeric abilities in animals? A study 1971 found that rats could be trained to approximate numbers. When rats were rewarded for pushing a lever a certain number of times, they tended to push the lever about the same number of times from then on. Many species are capable of discriminating quantities in approximate ways. In one experiment, when lionesses were played a recording of a lioness roaring, they tended to approach the source of the sound. However, when the sound of three lionesses was played, the lionesses tended to retreat from the source, an ability to differentiate that has obviously improved their survival odds. Some non-primates can exactly distinguish quantities in small sets. New Zealand robins have been shown to discriminate sets of up to four items, above that only if the ratio is at least 1:2, such as choosing between four and eight.
In some species, quantity discrimination seems to be based on continuous variables, so it’s often unclear whether quantity estimations are based on the greater size, density, or movement of the larger quantity. In one study, salamanders were given a choice between two containers of fruit flies. They consistently chose the container with the largest number of flies; but when the choice was between two selections of live crickets, the salamanders’ choice was based on the amount of movement among the observed insects.
For several decades, researchers have been studying the cognitive abilities of primates. It turns out that they share our ability to exactly recognize small quantities and our approximate recognition of larger quantities. In an experiment similar to one conducted with children, psychologists found that rhesus monkeys are capable of distinguishing quantities between 1 and 4 where the monkeys always chose the greater amount. For larger quantities, the monkeys were able to pick the greater amount only if there was a significant numerical difference between them. In other words, chimp selections were characterized by the same ratio effect observed in many other animals and in anumeric humans.
Chimps are also able to add quantities together. In one experiment, chimpanzees were given a choice between two trays; one tray had a pile of three treats and a pile of two treats, and the other tray had a pile of three treats and four treats. The chimps could recognize that the second tray (4 + 3) was greater than the first tray (3 + 2). In cases where the difference was small, say between 7 and 8, the chimps tended to make more mistakes. Researchers have shown that primates in captivity can also order symbols and recognize that each successive symbol represents a greater quantity. For example, rhesus monkeys can learn to touch numerals 1-9 on a computer screen in ascending order and can learn which quantity each number represents.
There is a clear relationship between number systems and subsistence strategies. Recent evidence confirms a correlation between simple numbers systems and hunter-gatherer cultures, and complex number systems and agricultural societies. Patience Epps of the University of Texas and her team of linguists studied hunter-gatherers in Australia and found that more than 80 percent of the languages spoken by this group have an upper numeric limit of just 3 or 4.
Large agricultural societies necessitated elaborate number systems, and both evolved together. Elaborate mathematical practices developed in Mesopotamia, China, and in Central America only after agricultural revolutions enabled food surpluses that allowed for mathematically trained classes of people in those regions. Unsurprisingly, numerals are common to all early forms of writing. Chinese writing from 3,000 years ago contain numerals showing such things as the number of enemy prisoners and the number of animals hunted. In Mesoamerica, some of the earliest forms of writing are lines and dots used for calendars. In Egypt, the oldest known hieroglyphics usually depict information about quantities of goods.
Numerals and higher number limits enabled new forms of agriculture and trade because they allowed for the exact discrimination of all relevant numeric quantities. The ease of representing precise quantities with lines and dots on multiple surfaces provided a foundation for more elaborate numerical representation, which led to writing and subsequent inventions in both the sciences and the arts. As societies evolved mathematics did as well: the facilitation of mathematical problem-solving meant the facilitation of architecture and science, and led eventually to modern cities and technology.
How did we ever manage to create names for quantities if we weren’t biologically “wired” for numbers? Everett suggests that “when some number-inventors happened upon the realization that words could be used to distinguish quantities like five from six, it enabled them to establish a new way of thinking about quantities that others began to adopt. Through that adoption, numbers spread.” And the rest, as they say, is history.

The First Word
The Search for the Origins of Language
Christine Kenneally
Human communication depends on the same genetic foundations as other animals. Some were born with a greater inclination to collaborate, forming the symbolic communication of language.
In the series: The Evolution of Language
Further Reading »
External Stories and Videos


Babylonian Numbers
Dr. Eleanor Robinson, University of Cambridge
Learn to write numbers using the Babylonian base-60 system.

