By Sally Mallam
Contributing Writer

They used prose, not poetry, as their language of inquiry, and gradually prose became associated with the language of investigation, and logos to stand for what we would call scientific inquiry.

Just as questions, debate and reasoned solutions were part of political discussions in the Greek polis, these men focused on speculative questions, discussions, debate and reasoned conclusions with regard to the nature of the world. They thought of themselves as philosophers (literally “lovers of wisdom”).

Rather than rely on supernatural answers, they sought the natural elements that were involved in the world’s formation (physis), and to identify the Eunomia (balance) of the universe and the principles governing it. Their questions fell into areas that we now categorize as science, philosophy and spirituality. They used prose, not poetry, as their language of inquiry, and gradually prose became associated with the language of investigation, and logos to stand for what we would call scientific inquiry. From this sense of the word we get “logic”—rational thinking.

In the first half of the sixth century, the Ionian city of Miletus was a rich trading center with numerous colonies, possibly the most powerful Greek city on the coast of Asia Minor (modern-day Turkey). Its citizens were audacious sailors whose travels took them to the cultures of Mesopotamia and Egypt and who lived close to the rich city-state of Lydia.

Thales of Miletus (Circa 624–547 BCE)

It was the Ionian mathematician and astronomer Thales, whom Aristotle called “the founder of natural philosophy,” who set up the Milesian school and so launched the beginning of philosophy and science. Thales was from a wealthy family in Miletus whose father may have been of Phoenician ancestry. He was a contemporary of Solon and had also traveled and studied in Egypt, where he may well have learned some of the mathematical discoveries with which he is credited. Thales was widely believed to have predicted the solar eclipse in 585 BCE. He was a highly successful businessman and statesman, as well as a mathematician who is said to have claimed his only interest in business was to demonstrate the practical advantages of clear thinking.

Never before had someone put forward general ideas and explanations about the nature of the world without recourse to religion or myths. For the first time there was a conviction that there were natural laws controlling nature, and that these laws were discoverable. The world is made of material, and it is governed by the laws of material motion. Thales did not break entirely with religious explanations but he did attempt to give rational explanations for physical phenomena, claiming that behind the phenomena was not a catalogue of deities, but one single, first principle, which he called an archê, “cause.” He identified this first principle as water.

Anaximander (Circa 611–547 BCE)

He was Thales’s student and was the first to write a treatise in prose, which is known traditionally as On Nature. This has been lost, although it probably was available in the library of the Lyceum at the times of Aristotle and his successor Theophrastus. He explored the notion that there was a single, imperishable, primary element, but he disagreed with Thales over what it was. It was hard to see how water could be contained in something that is very dry, for instance, and Anaximander went on to reason that the fundamental material must be something that transcends ordinary matter, all of which would have limitations similar to the water theory. Therefore he postulated that the fundamental material must be something imperceptible to our senses that encompasses even properties of matter that appear opposite from each other. Anaximander identified this with “the Boundless” or “the Unlimited” (Greek: apeiron, i.e., “that which has no boundaries”). It lay beyond our experience, it was beyond the gods and the source of all life.

Another Milesian, Anaximenes (ca 585–525 BCE), said the primary element was air.

Pythagoras (Circa 582–504 BCE)

He was active in southern Italy towards the end of the sixth century. He coined the term “lovers of wisdom” (philo-sophia), saying that some people seek wealth, some power and admiration, and some fame, but the wisest are those who pursue knowledge: the philosophers. He wrote nothing down and apparently discouraged writing, so we have no original documentation. Nevertheless, in common with many other Axial Age thinkers, it appears that he and his pupils’ primary quest was for spiritual enlightenment.

Pythagoras was well traveled. As a young man he studied with both Anaximander and Thales of Miletus. He was said to have been initiated into the ancient mysteries of the Phoenicians studying in the temples of Tyre, Sidon, and Byblos in modern-day Lebanon, and to have visited Haifa and the temple on Mount Carmel in Israel. He spent time studying in Egypt, and when the Persian Empire, expanding westward, invaded that country, he was captured along with members of the Egyptian priesthood and taken to Babylon. In Babylon he would have found himself at the center of a convergence of religious and philosophical ideas, and in a culture that, like Egypt, was also at the forefront of mathematics and astronomy. Zoroastrianism was in its early days, the Magi (Zoroastrian priests) were establishing the ethical teachings, rituals and monotheism of their religion in contrast to the multiple gods and rigid social hierarchy that was already part of Babylonian culture. Here Pythagoras may well have studied the importance of numbers and of the interaction of contraries or opposites—good/evil, positive/negative, light/dark, right/wrong, and so forth.

After twelve years in Babylon, he was allowed to return to his birthplace—Samos in Ionia. Leaving Babylon, he may well have traveled through Persia into India to continue his education, where some sources say he is referred to as Yavanacharya, the “Ionian Teacher.” He could well have obtained his Karmic ideas directly from India, although similar ideas were also known in Egypt, plus, in Greece, the Orphic cult was heavily influenced by Eastern belief, particularly on the transmigration of the soul.

He intended to set up a community in Samos but corruption, neglect and tyrannical oppression made it unsuitable. He journeyed to Croton on the east of Italy, where he founded the Pythagorean society of philosophy, mathematics, and natural sciences. People from different classes—and even women—came to his school to hear his lectures and become part of his community. He recommended modesty, austerity, patience, equality and self-control.

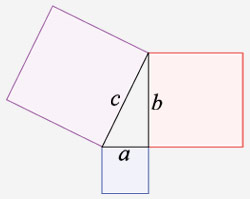
Pythagoras’s famous saying “All is number” refers to his understanding that beyond the world of appearances there lies an abstract harmonious world of number. For the first time he demonstrated that the structure of nature is translatable into numbers and geometric forms which can describe its fundamental laws.

John Strohmeier and Peter Westbrook write in their book Divine Harmony–The Life and Teachings of Pythagoras, “For Pythagoras, mathematics served as a bridge between the visible and invisible worlds. He pursued the discipline of mathematics not only as a way of understanding and manipulating nature, but also as a means of turning the mind away from the physical world, which he held to be transitory and unreal, and leading it to the contemplation of eternal and truly existing things that never vary. He taught his students that by focusing on the elements of mathematics, they could calm and purify the mind, and ultimately, through disciplined effort, experience true happiness.”

Heraclitus of Ephesus (Circa 535–475 BCE)

He was a student of Pythagoras. He wrote that “all is flux,” that truth lies in constant change, in the impermanence of nature as illustrated by the saying attributed to him: “No man steps into the same river twice.” You could not rely on the evidence of your senses, you needed to go deeper in order to find unity. At the foundation of this perpetual flux experienced by both human beings and nature was the ruling principle—logos.

Xenophanes (Circa 560–480 BCE)

He went to Elea from Asia Minor where he founded the Eleatic School. By this time, people now realized that political institutions could be changed without causing any reaction from the gods, and some now began to question their existence. Xenophanes ridiculed these anthropomorphic gods, he believed in one great god, which was not physical but was all mind (in Greek: nous), moving all things by the force of his spirit without himself having to move.

Parmenides of Elea (Circa 520–450 BCE)

He was a student of Xenophanes. He taught that reality was one complete, eternal, quintessential Being beyond time and change, and that the changing world registered by our senses was an illusion.

Anaxagoras of Athens (Circa 500–428 BCE)

He taught that all things come to be from the mixing of innumerable tiny particles of substance, shaped and controlled by a creating principle he called Nous (“mind”), a divine intelligence.

Leucippus (5th century) and Democritus (Circa 460–370 BCE)

They argued that everything was made up of an infinite number of tiny, invisible particles which they called “atoms.” Democritus named the atom after the Greek word atomos, which means “that which can’t be divided further.” As they move in infinite space, these atoms combine with others into an innumerable variety of shapes, forming, among other things, what we see and know of the world. Man’s actions are no exception to this universal law, and free will is a delusion.

Epicurus (341–270 BCE)

Like Democritus, Epicurus also taught that the universe was made of tiny indivisible units, or atoms, moving in infinite space. Everything that occurs is the result of these atoms colliding, rebounding and joining with each other, in a ceaseless process of creation and destruction. Plants, animals and humans evolved randomly over ages, some forming species that survive for a time, but nothing lasts forever. Only atoms are immortal, so every phenomenon is the result of natural causes. The atoms in the void obey the law of their own natures, falling downwards because of their weight, meeting and clashing, forming molecules and larger masses, and, ultimately, building up the whole universe of worlds in infinite space.

In this view then, there is no need of gods, who are similarly created but are unconcerned with human affairs, so should not be feared. Neither should death be feared since it is just the dissolving of the atoms that make up the body and soul.

However, Epicurus’s philosophy differed from the earlier atomism of Democritus in that he believed that our senses are infallible, and through them, we know that we have free will. If man’s will is free, it cannot be by special exemption to the natural laws of atomic materialism, but because of some inherent principle: some element of unconscious spontaneity in the atoms’ behavior. Epicurus’s conclusion was that they randomly swerved. “It is the ‘swerve’ then which enables the atoms to meet in their downward fall, it is the ‘swerve’ which preserves in inorganic nature that curious element of spontaneity which we call chance, and it is the ‘swerve’, become conscious in the sensitive aggregate of the atoms of the mind, which secures man’s freedom of action and makes it possible to urge on him a theory of conduct.” (Lucretius)

This conduct should be guided by each individual’s perception of pleasure and pain, experienced in both body and soul. Pain is the dislocation of atomic arrangements and motions, pleasure their readjustment and equilibrium. Epicurus’s objective was to attain a balanced, tranquil life, characterized by ataraxia—peace and freedom from fear—and aponia—the absence of pain. Pleasure to Epicurus was attained when one is free from either want or pain: when both have been removed.

His extensive writings were mostly lost and suppressed by Christian and Jewish theologians to the extent that the English definition of Epicurean means indulgence in sensual pleasures, especially eating and drinking, and his name is one of the words for heresy in Hebrew. His works survived mostly because of a 7,400 line poem about them, On the Nature of Things by the Roman poet Lucretius.

Some of Epicurus’ teachings include:

“Death is nothing to us. When you are dead you will not care, because you will not exist.”

“All organized religions are superstitious delusions rooted in longings, fears, and ignorance.”

“The greatest obstacle to pleasure is not pain; it is delusion. The enemies of human happiness are inordinate desire—the fantasy of attaining something that exceeds what the finite mortal world allows—and gnawing fear.”

The Sophists

As part of the scientific revolution in the fifth century BCE, a new class of teachers appeared, who taught epistemology, language, geometry, astronomy and biology, and above all, rhetoric and eristic—the study of argumentation. Anyone who wanted a position of importance, especially in a democracy, would have to have oratorical skill, strength in debate, and a knowledge of law and politics; one would need to know how to manage property and maybe run the state, and know something of music, astronomy, math, physics, and so on. The Sophists equipped one to be a leading citizen, and supplied answers to help people live in a world whose reality had now been somewhat undermined by the Pre-Socratics.